How shall we proceed to bring general relativity and quantum mechanics together? We’ll start with a basic component of relativity, the metric tensor. This is the mathematical way to describe time and distance, along with how they bend. General relativity uses this metric to describe what massive objects do to spacetime, and what spacetime does to massive objects. A change in the metric (ds2) is described in terms of a change in time (dt2) and a change in space (dr2 + r2dΩ2) as:
ds2 = -(dt2)+(dr2 + r2dΩ2)
All changes caused by massive objects are continuous and smooth.
Fields are a set of numbers with a set of values defined everywhere. They are used in the Standard Model of Particle Physics to describe particles: one field is used to describe electrons, another field is used to describe top quarks, and so on, for each and every different kind of particle. Quantum mechanics describes variations in the values of the field, and these fluctuations of the “quantum field” explain where particles are, where they are going, and their properties.
We introduce quantum mechanics to general relativity with a simple kind of quantum field which has just one value (a scalar) everywhere. Let’s call this field φ and say that it has tiny variations that change the space part of the metric like this:
ds2 = -(dt2)+ (1- φ )(dr2 + r2dΩ2)
When φ is zero everywhere, there is no change in the metric. The new effect we are looking for is when φ has (very small) variations that change the “size” of the metric randomly.
Most importantly, models of quantum gravity predict these kinds of fluctuations to explain what gravity is. Since it yields the same predictions as general relativity, there is nothing new for us to test with gravity directly, but there are interesting “side effects” of this φ field that we can observe. So, if we see these effects, we are in a much better position to explain what gravity is. What are the side effects we seek?
The minute fluctuation in φ which give rise to gravity also causes a photon of initial wavelength 𝛌0 to accumulate changes in wavelength, energy, and phase as it swims through the modified metric. The interferometers we are building for GQuEST will be sensitive to these tiny changes.
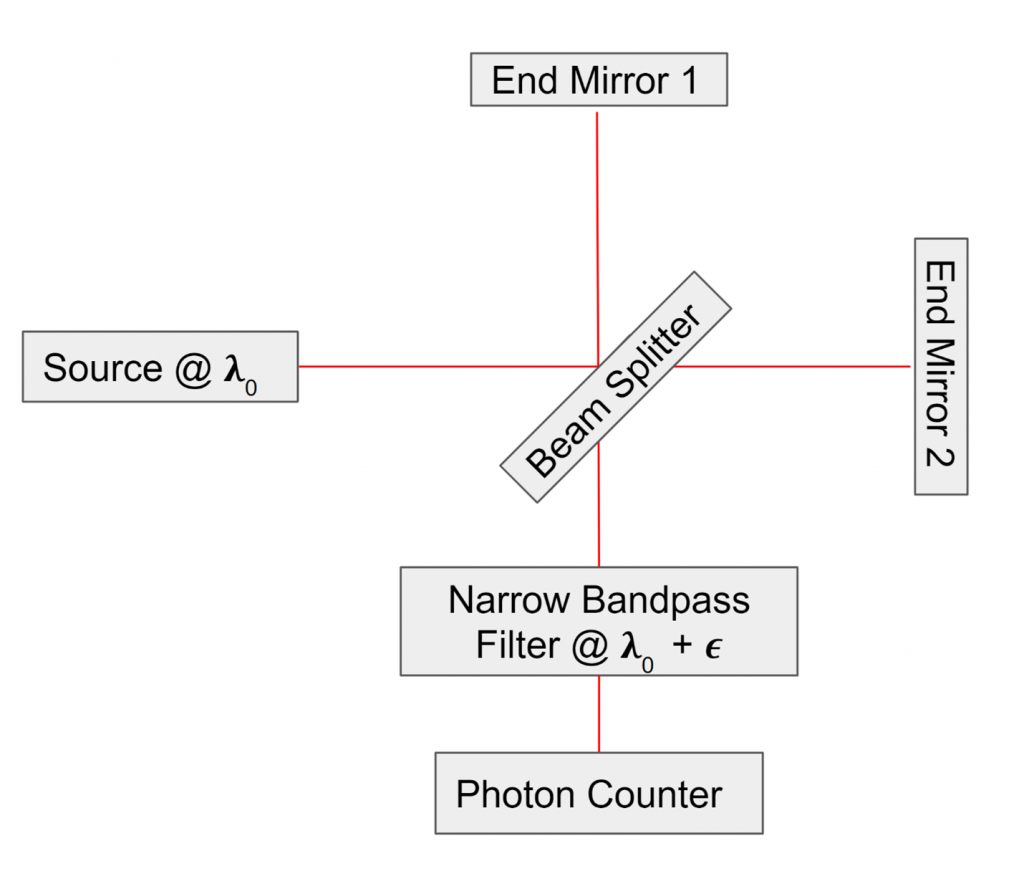
This sketch illustrates the GQuEST strategy:
In this arrangement, photons from the source laser at wavelength 𝛌0 meet the beam splitter. The photon’s state propagates up to End Mirror 1 and to the right to End Mirror 2. After reflection, these states recombine at the beam splitter.
The interferometer is set up so that a small fraction of the input photons will be reflected down. We are only interested in photons which have accumulated larger changes in wavelength and phase. To distinguish these, we use a narrow passband filter offset a small amount from 𝛌0 and count signal photons that pass this filter.
